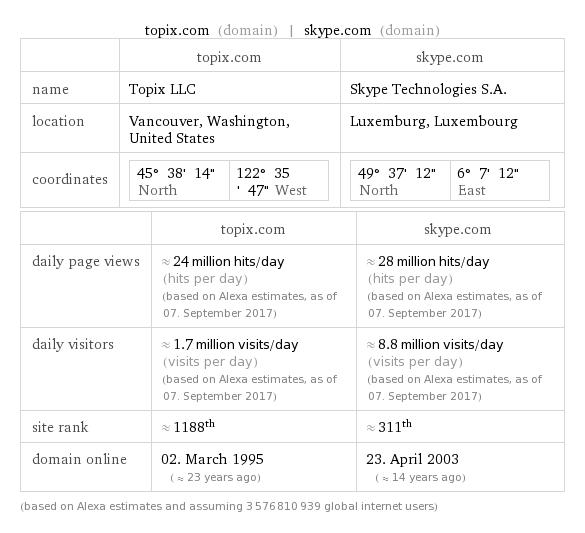
Taylor series of sqrt(1+x)
| Input interpretation |
|---|
| series | sqrt(1 + x) |
| Series expansion at x=0 |
| 1 + x/2 – x^2/8 + x^3/16 – (5 x^4)/128 + (7 x^5)/256 + O(x^6) (Taylor series) (converges when abs(x)<1) |
| Series expansion at x=∞ |
| sqrt(x) + sqrt(1/x)/2 – 1/8 (1/x)^(3/2) + 1/16 (1/x)^(5/2) – 5/128 (1/x)^(7/2) + O((1/x)^4) (Puiseux series) |
| Approximations about x=0 up to order 3 |
| (order n approximation shown with n dots) |