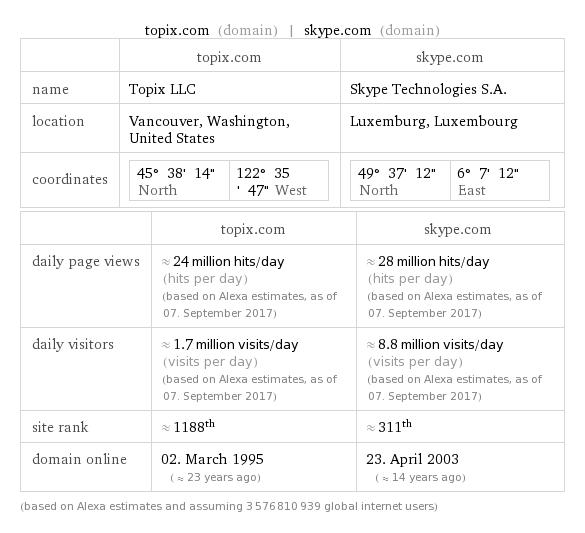
Sqrt(1+x^2)
| Input |
|---|
| sqrt(1 + x^2) |
| Series expansion at x=0 |
| 1 + x^2/2 – x^4/8 + O(x^5) (Taylor series) |
| Series expansion at x=-i |
| sqrt(2 – 2 i x) + (i sqrt(1 – i x) (x + i))/(2 sqrt(2)) + (sqrt(1 – i x) (x + i)^2)/(16 sqrt(2)) – (i sqrt(1 – i x) (x + i)^3)/(64 sqrt(2)) – (5 sqrt(1 – i x) (x + i)^4)/(1024 sqrt(2)) + O((x + i)^5) (generalized Puiseux series) |
| Series expansion at x=i |
| sqrt(2 + 2 i x) – (i sqrt(1 + i x) (x – i))/(2 sqrt(2)) + (sqrt(1 + i x) (x – i)^2)/(16 sqrt(2)) + (i sqrt(1 + i x) (x – i)^3)/(64 sqrt(2)) – (5 sqrt(1 + i x) (x – i)^4)/(1024 sqrt(2)) + O((x – i)^5) (generalized Puiseux series) |
| Series expansion at x=∞ |
| x + 1/(2 x) – 1/(8 x^3) + O((1/x)^4) (Laurent series) |
| Derivative |
| d/dx(sqrt(1 + x^2)) = x/sqrt(x^2 + 1) |
| Indefinite integral |
| integral sqrt(1 + x^2) dx = 1/2 (sqrt(x^2 + 1) x + sinh^(-1)(x)) + constant |
| Global minimum |
| min{sqrt(1 + x^2)} = 1 at x = 0 |