1/sqrt(1-x^2)
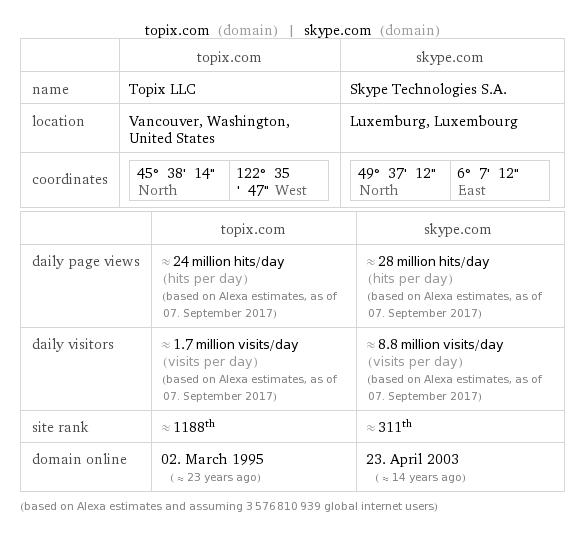
| Input |
|---|
| 1/sqrt(1 – x^2) |
| Alternate form |
| 1/(sqrt(1 – x) sqrt(x + 1)) |
| Roots |
| (no roots exist) |
| Series expansion at x=-1 |
| 1/(sqrt(2) sqrt(x + 1)) + sqrt(x + 1)/(4 sqrt(2)) + (3 (x + 1)^(3/2))/(32 sqrt(2)) + (5 (x + 1)^(5/2))/(128 sqrt(2)) + O((x + 1)^(7/2)) (Puiseux series) |
| Series expansion at x=0 |
| 1 + x^2/2 + (3 x^4)/8 + O(x^5) (Taylor series) |
| Series expansion at x=1 |
| 1/sqrt(2 – 2 x) – (x – 1)/(4 sqrt(2 – 2 x)) + (3 (x – 1)^2)/(32 sqrt(2 – 2 x)) – (5 (x – 1)^3)/(128 sqrt(2 – 2 x)) + (35 (x – 1)^4)/(2048 sqrt(2 – 2 x)) + O((x – 1)^5) (generalized Puiseux series) |
| Series expansion at x=∞ |
| 1/sqrt(-x^2) + 1/(2 sqrt(-x^2) x^2) + 3/(8 sqrt(-x^2) x^4) + O((1/x)^5) (generalized Puiseux series) |
| Derivative |
| d/dx(1/sqrt(1 – x^2)) = x/(1 – x^2)^(3/2) |
| Indefinite integral |
| integral 1/sqrt(1 – x^2) dx = sin^(-1)(x) + constant |
| Global minimum |
| min{1/sqrt(1 – x^2)} = 1 at x = 0 |
| Limit |
| lim_(x-> ± infinity) 1/sqrt(1 – x^2) = 0 |